Qualitative Evidence of Student Growth
As discussed in the section on quantitative evidence of student growth, the i-Ready diagnostic does not assess students' problem-solving processes or abilities to describe mathematical thinking. However, these skills are essential for math students, so it is crucial that educators develop other ways to assess them. I ask students to explain their thinking verbally every day in class, and many of the formative and summative assessments they complete involve written components. However, this year I also developed a new sort of task that assesses students' abilities to approach unfamiliar problems with flexible thinking and reflective metacognition. As such, I have spent a good deal of time this semester helping my students to learning strategies for tackling challenging new problems. The links below will provide details about some of the teaching strategies that I have used during this process and examples of student growth in responding to unfamiliar prompts over the course of the semester.
Brain-Targeted Teaching
During the Effective Practices in Teaching and Learning II course, degree candidates learn about brain-targeted teaching. Since learning about this model for education, I have attempted to integrate its principles into my approach to unit planning. These principles are detailed in the presentation I prepared for Effective Practices II about my first brain-targeted unit plan.
Brain-Targeted Teaching Unit Plan. This plan was previously submitted as an assignment for Effective Practices in Teaching and Learning II in the spring of 2017. The principles and strategies it details are illustrative of the approach I now use for planning all of my units and structuring my classroom environment. The brain-targeted teaching approach has been particularly useful in visualizing a warm, welcoming classroom learning space and planning strategies to help students remember key information in fun, accessible ways.
Teaching Strategies: Flexible Problem-Solving
I always try to present math as the study of patterns and puzzles, and I periodically challenge students with problems that look complicated but become much easier when one's perspective changes. For example, I like to ask students how many games will be played in the March Madness basketball tournament, which begins with 64 teams spread across the four quadrants of a giant bracket. Every student I have had approaches this by computing the number of games that would be played in the first round (32), then the number of games that would be played in the second round (16), etc. The sum of all of these numbers (i.e., 32, 16, 8, 4, 2, and 1) is 63. However, the problem becomes much easier when one makes the simple adjustment of focusing on losses rather than on wins. A team is eliminated if it loses one game, and 63 of the 64 teams must lose in order to crown a single winner, so 63 games must be played. Questions like this helped students to appreciate the value of considering multiple perspectives when solving problems.
As students learn to analyze problems from multiple perspectives, they become much better at approaching questions that seem unfamiliar to them. However, this is a very gradual learning process. Most middle schoolers initially struggle to employ even one problem-solving strategy when presented with a novel task, and almost none do a good job of explaining their thinking in writing as they do so. Indeed, it is quite common for students to "shut down" when confronted with a totally unfamiliar problem for the first time.
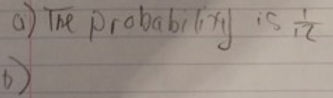
Student "shut-down" in response to a novel probability problem. The student had 15 minutes to attempt the problem and produced only the work shown to the left. Although this is an extreme example, it is quite common for students to become intimidated by challenging, unfamiliar problems. Educators must explicitly teach scholars strategies for engaging with such tasks.
Interestingly, students are much less likely to give up on a task when working with a group. Seeing that other scholars are struggling with the same problem can be empowering and create a safer space in which to take intellectual risks. As a result, many of my teaching strategies for tackling tricky problems begin by facilitating small-group discussions. For example, I love to challenge groups to create a list of approaches that they could take when confronting new types of math problems. Presenting this as a brainstorming topic helps lower the stakes for students; they need not apply the strategies to a specific task, but rather build a toolbox that they could use for future tasks.


Examples of group brainstorming of strategies for solving novel problems. I am always fascinated to see the extent of the overlap between different groups' lists. For example, most groups recognize the potential benefits of identifying important information and vocabulary within the problem, making connections to prior knowledge, searching for patterns that might be helpful, and creating labeled visualizations.
As described on the page about building the broader mental habit of thinking flexibly, I also utilize peer evaluation and group problem-solving as teaching techniques to help students build comfort with unfamiliar problems. Just as creating a list of strategies can feel like a lower-stakes task than employing them on an actual problem, being evaluated by a peer usually feels less stressful for students. They strive to give each other constructive feedback and build familiarity with the rubric, but the exercise feels less official (and less likely to have a negative impact on their grades) than receiving feedback directly from me. Similarly, solving a problem with a team is a great way to try new approaches and see what works without feeling like a test of some sort is being administered.
Clearly, then, I strive to create safe spaces for students to explore problem-solving strategies before asking them to complete any sort of teacher-graded assessment of their abilities. This allows them to practice strategies and feel like their skills are being appropriately recognized and rewarded when they complete a challenging task for a grade. And, as the samples in the next section show, my students have improved greatly on their ability to handle novel problems.
Student Growth Samples
Below are PDFs with work samples from four of my students. Each document contains student answers for three different tasks, and each set of answers is followed by a teacher-completed rubric that awards points for correct, clearly-explained answers. The three tasks to which the students responded for these work samples are reproduced below and in each PDF. Task A was administered in February, Task B in March, and Task C in April. All three come from Illustrative Mathematics' publicly-available library of rich math tasks, and all three are designed for high-school students who have had significantly more exposure to probability, functions, and algebra than any of my students have had.
Task A (February)
Cecil has two six-sided dice, a red one and a white one.
a. If Cecil throws the two dice, what is the probability that the red die is a 1? What is the probability that the sum of the dice is 7?
b. Are the two events described in part (a) independent? Explain.
c. What is the probability that the red die is a 2? What is the probability that the sum of the two dice is 10?
d. Are the two events described in part (c) independent? Explain.
Task B (March)
Imagine Scott stood at zero on a life-sized number line. His friend flipped a coin 50 times. When the coin came up heads, he moved one unit to the right. When the coin came up tails, he moved one unit to the left. After each flip of the coin, Scott's friend recorded his position on the number line.
a. Let f assign to the whole number n, when 1≤n≤50, Scott's position on the number line after the nth coin flip. Explain why f is a function.
b. Write a sentence explaining what f(5)=5 means in everyday language.
c. Before Scott began the random walk, he asked his friend to calculate the probability that f(3)=0. What should his friend respond?
Task C (April)
Suppose P and Q give the sizes of two different animal populations, where Q>P. In (a)–(f), say which of the given pair of expressions is larger. Briefly explain your reasoning in terms of the two populations.
a. P+Q and 2P
b. P/(P+Q) and (P+Q)/2
c. (Q−P)/2 and Q−P/2
d. P+50t and Q+50t
e. P(P+Q) and 0.5
f. P/Q and Q/P
Scholar A
This scholar had a very low score on the first novel task and improved substantially over the subsequent months. He is still working on explaining his answers fully in words. He is getting much better at showing his work mathematically, though, and he has made dramatic growth on this metric by any standard.

Scholar B
This scholar also had a fairly low score on the first task, which proved to be a powerful motivator for him. He quickly internalized the importance of explaining his work fully, and his two subsequent assessments are exemplars in every way.

Scholar C
This scholar's score on the first task was slightly better than the first two students,' but her growth from the first task to the second was much less dramatic. However, her written explanations improved steadily and significantly after the first task, and they are truly excellent in the third task. Her score for correct solutions on this final task is also great.

Scholar D
This scholar is one of my brightest, and his initial score was quite high despite the fact that the task was unfamiliar and intended for high schoolers. However, he often skips steps and struggles to put his thinking into words. He and I worked intensively to build upon the success that he had with part (c) of the second task, and his work on the third task really speaks for itself.
