Thinking Flexibly
Flexible thinking is arguably one of the most important habits of mind for a budding mathematician. I try to help my students understand math as the study of patterns and puzzles, both of which tend to require a certain degree of mental flexibility to solve. As a result, much of my teaching about flexible thinking is integrated directly into the math curriculum that I use. That said, I do make an effort to include explicit flexible thinking activities in my plans for the first few days of the school year. For example, I love to challenge students to build the tallest structure they can using only a dozen pipe cleaners or a few sticks of spaghetti and a marshmallow. I also carefully intersperse math brain teasers and pattern games into logistical presentations about school rules, schedules, etc. I want my scholars to be ready to use flexible problem-solving strategies at any moment. In addition, there are many excellent resources for teaching flexible thinking as a topic unto itself. I have used several aspects of the lesson plan below, including its scholar-friendly "S.O.D.A.S." (Situation, Options, Disadvantages, Advantages, Solution) framework for finding flexible approaches to challenges, and I may well teach it in its entirety at the beginning of next year.
A slideshow explaining our new schedule for the year. Note that slides 6, 9, and 12 all contain pattern problems and math brain teasers. I introduce these as miniature competitions, which students really enjoy, and they help me to get a sense of which scholars are already strong flexible thinkers and which may need extra support to develop the habit of mind.
An excellent lesson about thinking flexibly. I have borrowed both the "S.O.D.A.S" framework and the famous gestalt shift image on the final page for various lessons, and I have wanted to find a day when it makes sense to work through the full lesson for quite a while.
Most of my students begin the year wanting to learn clear strategies for solving a problem before they are asked to do so on their own. As such, they often get overwhelmed when they are forced to confront a novel mathematical situation. Of course, most of the mathematical situations they encounter in real life will seem novel at some point, and I want to ensure that I am helping them develop into careful mathematical thinkers who can handle such challenges with logic rather than trepidation. Thinking flexibly, therefore, is a natural habit of mind to teach on virtually every day of math class.
For example, flexible thought processes relate very naturally to the study of equivalent expressions. There are many different ways to describe any set of mathematical operations. For example, the expression 2x-5 could be written as “double a number x decreased by 5,” “five less than the product of x and 2,” “the difference between twice x and 5,” etc. This flexible notation forces students to confront ambiguity and embrace alternative ways to describe and think about mathematical quantities. However, the notion of seeking multiple correct solutions initially presents a conceptual challenge for many of my students (especially sixth graders). Thus, it is logical to connect it with the comparatively familiar habit of flexible thinking, which my scholars discuss and practice during every unit.
For instance, during one class period in our equivalent expressions unit, we started with a brainstorming exercise in which students tried to identify as many words as they could that were associated with addition, subtraction, multiplication, division, equality, and parentheses. This introduction, which aligned with both the core content of the lesson and the idea of thinking flexibly, reinforced the notion that there could be many mathematically valid ways to describe the same quantity. During this exercise and throughout the lesson, I was very intentional about offering explicit praise for students who thought flexibly enough to offer equivalent expressions for correct answers. This set my students up to succeed later in the class period, when I challenged them to write their own word problems based on expressions with variables as a way to deepen their conceptual mastery. The exercise of creating a story that could be modeled with an expression like (3d-1)/2 requires flexible, creative thinking. It is just this sort of thinking that supports deeper understanding of mathematical processes and provides students with access points for higher-level problems.
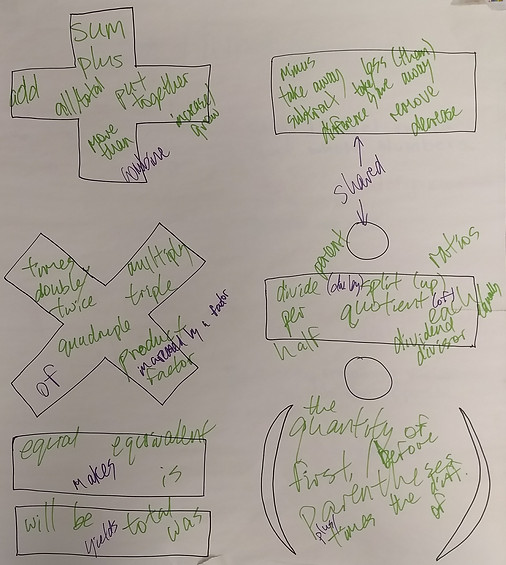
The results of scholars' brainstorming about different terms for the same operations. I was impressed to see how effectively this activity engaged my shyer scholars, who volunteered much more enthusiastically than usual to offer equivalent expressions. The emphasis on flexible thinking—and the praise that accompanied it all class—led directly to increased student participation about different ways to communicate the same information.
One of the first words I teach students at the beginning of each year is "autonomy," and I regularly remind them that they have autonomy in selecting problem-solving strategies that work for them on any given problem. To underscore this theme, I often frame the notes that my students take in terms of flexible thinking. We work through multiple different methods for solving problems and then I encourage them to use whichever feels most comfortable to them on a set of examples. This approach provides access points that are compatible with a wide range of learning styles and shows students that there are many different, equally valid ways to tackle math problems.

"Autonomy" is literally among the first words that my students see as they walk into my classroom. I make a point of celebrating scholars' autonomy to choose solution strategies that work for them, flexible ideas about how to approach problems, and mistakes made while trying new, innovative approaches to their work.
Three different methods for solving percentage problems. After we worked through a problem using each of the methods as a class, students practiced in small groups and on their own using the methods that they found most convenient for handling different sorts of word problems.
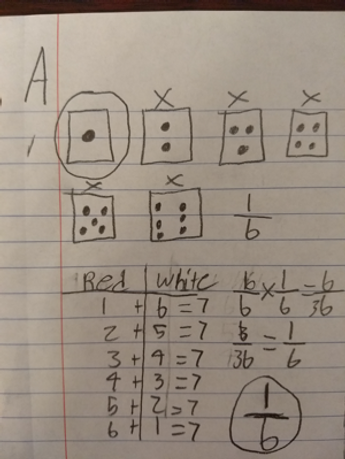
To teach and assess flexible thinking this year, I designed an activity in which students are presented with an unfamiliar math task. They have never explicitly learned how to solve this problem; indeed, they may not even know all of the math vocabulary words in it. Thus, they cannot hope to arrive at a solution by simply applying algorithmic strategies we have learned in class. Instead, I ask them to try multiple strategies to solve the problem and ensure that anyone reading their responses can understand their thinking. Encouraging students to pursue new lines of thinking—even those that are clearly incorrect—is a great way to model and advocate for flexible thinking.



Student work samples from the initial flexible thinking task. At the top left and the right are examples of scholars who worked hard but did not adequately explain their thinking. At the bottom left is a typical response from a scholar who felt intimidated and gave up on the task.
During a subsequent class period, I give each scholar a rubric and a paper from one of his or her peers. Because my scholars are used to working interdependently with each other, they are excellent peer assessors who work diligently to give each other fair scores. Peer evaluation offers a number of benefits for my scholars. First of all, seeing other people’s strategies leads to a lot of “aha” moments for scholars, which adds to the set of strategies that they can use on new problems they encounter. Furthermore, students whose initial reaction to the activity is to give up quickly understand that the rubric rewards persistence. Similarly, scholars who repeatedly try one solution strategy realize that their scores would be higher if they were to adopt a more flexible approach and test multiple different methods for solving the problem.
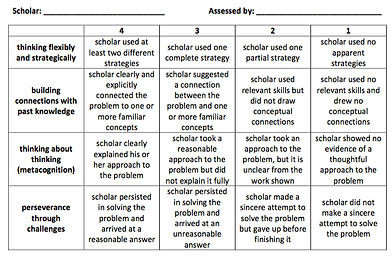

Peer evaluation rubrics. Students assess the degree to which their classmates have thought flexibly and strategically, built connections with past knowledge, thought about thinking, and persevered through challenges. I designed this rubric with explicit reference to the 16 habits of mind. As such, it aligns with much of my habits and mindsets teaching vocabulary.

After peer evaluation, students may be asked to complete the task again in an effort to improve their scores by thinking more flexibly. However, the more common focus after peer assessment is on metacognition. I group scholars based on their initial responses to create heterogeneous teams who have tried different approaches and arrived at different answers. I then facilitate group conversation about the problem with two distinct goals in mind. First, the team must create a list of strategies that math students can use when faced with an unfamiliar, challenging problem. It is always fascinating to see the extent of the overlap between different groups’ lists. For example, nearly every group recognizes the potential benefits of identifying important information and vocabulary within the problem, making connections to prior knowledge, searching for patterns that might be helpful, and creating labeled visualizations.
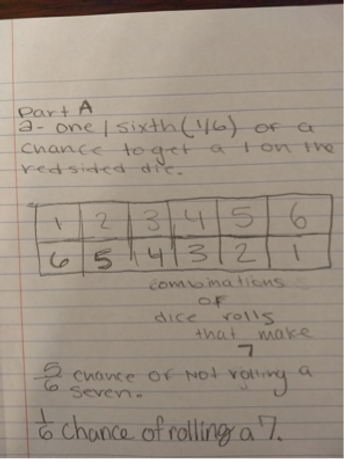
The second goal is to solve the problem again as a team. I urge groups to identify explicitly the strategies they are using and show evidence of all of the thinking behind each step in their written responses. Groups invariably produce clearer, better-reasoned responses to the problem, despite the fact that they have still received no explicit instruction about how to solve it. This helps them to realize that the primary shift is in the way they are thinking about their mathematical reasoning and how they can explain that to others. For further information about my use of this task to teach students about the benefits of thinking flexibly, please visit my page on qualitative measurement of dramatic academic growth.
Samples of group solutions to an unfamiliar task. These responses are significantly easier to follow than any of the ones I received during the individual phase of this assignment. Students intentionally applied strategies like creating visual models of the problem and utilizing patterns that they found in those models. Moreover, they labeled and explained their work so that it was easy for readers to follow their logic, which demonstrates a newfound level of metacognition for most of them.
Thinking flexibly may integrate well with mathematical study, but it can also be reinforced through activities that are unrelated to core academic content. Presenting students with any sort of creative problem-solving challenge provides an opportunity for them to think flexibly about possible solutions. I love to have such creative challenges on-hand, and one of my favorites involves prioritizing a list of survival items after a plane crash in winter. I had used the activity before learning about habits of mind explicitly, and I have since added a habits-oriented reflection component that strengthens its pedagogical value substantially.
Examples of the flexible thinking wilderness survival challenge. The ranking that students create is not nearly as important as their justifications and reflections. Curious readers may be pleased to learn that pages 19-20 contain a plausible ranking of these items' efficacy in a survival situation.

Student graphic organizer about how flexible thinking looks, sounds, and feels in the classroom. This "Y-Chart" was made and presented as a group activity during one of our weekly community meetings.